Le surfaces NURBS (pour "Non Uniform Rational B-Splines") sont des surfaces, comme des plans, des surfaces côniques ou des surfaces cylindriques. Nous évitons à dessein les termes "cônes" ou "cylindres", qui évoquent des solides, c'est à dire des zones de l'espace délimitées par des surfaces. Le terme "surface" est défini comme un sous-espace de dimension deux séparant deux zones, que l'on nommera par commodité Z1 et Z2, de l'espace de dimension trois dans lequel elles se développent.
Si cette définition vous semble un peu formelle et compliquée, employons des exemples. Dans le cas bassement matériel qui nous occupe, l'espace est celui dans lequel notre existence se déroule, et plus particulièrement celui dans lequel un bateau navigue. Un plan horizontal est par exemple la surface de l'eau, qui sépare la zone Z1 (l'eau) de la zone Z2 (l'air). Cette définition n'est évidemment qu'une approximation, puisqu'on sait que cette surface est déformée localement par des vagues, et qu'à l'échelle d'une planète, il s'agit d'une surface sphérique... Un cylindre, tel qu'un mat, de bateau, est un solide délimité par la surface extérieure du mât, cylindrique en première approximation. Autre exemple. La forme de carène d'un bateau, est une surface. Elle a une épaisseur nulle. Par contre, la coque du bateau, en temps que solide, est limitée par deux surfaces avec de la matière entre les deux, par exemple quelques millimètres de composite. La surface de carène sépare donc la zone Z1 (eau, air) de la zone Z2 (composite).
Les surfaces sont donc des entités mathématiques de dimension deux plongées dans un espace de dimension trois. De la même manière, des courbes sont des entités mathématiques de dimension un, qui se développent dans l'espace de dimension trois. Le cas qui va nous intéresser est celui de courbes qui sont elles mêmes inscrites dans une surface. En reprenant les exemples ci-dessus, les parallèles et les méridiens, supposés tracés à la surface de l'eau, sont des courbes tracées sur cette surface. En approximation locale, des droites, à l'échelle planétaire, des cercles. Les "génératrices" du mât cylindrique d'un bateau, des droites tracées parallèlement à l'axe sur la surface du mât, sont aussi des courbes . La "ligne de bouchain" ou le "livet" d'une carène sont des courbes qui sont inscrites dans la surface de carène du bateau.
Dans ce site, les surfaces qu'on va considérer sont de l'espéce dite "surfaces paramétriques". Leur définition est qu'elles sont engendrées par des familles de courbes paramétriques.
Si nous reprenons les exemples ci-dessus, la surface de la mer peut être considérée comme une sphère engendrée par un grand cercle (médidien) que l'on fait tourner autour de l'axe de la planète. Localement, dans votre zone de navigation favorite, cela se traduit par le déplacement d'une droite (le méridien de la carte) le long d'une autre droite (le parallèle de la carte). Mais rien ne vous empêche de considérer qu'il s'agit d'un parallèle déplacé le long d'un méridien. La surface de l'eau dans cette zone est une "surface paramétrique" : chaque point de cette surface peut être définie, et cela de manière unique, dans l'espace habituel à trois dimensions, par deux paramètres : la latitude et la longitude.
La troisième dimension, dans cet exemple, est caractérisée par un paramètre qui est l'altitude : pour les marins, il a la propriété d'être habituellement nul. Il peut, c'est vrai, devenir négatif, ce qui est toujours considéré comme de très mauvais goût... Mais il faut bien considérer que cela peut arriver : la meilleure preuve est que les récepteurs "GPS" sur les bateaux affichent l'altitude ! Que le skipper qui n'a jamais demandé à un équipier de lire la notice du GPS tout en surveillant ce paramètre me jette la première règle Cras.
Dans l'exemple du mât, les courbes qui l'engendrent sont les génératrices (droites tracées parallèlement à l'axe du mât), et les sections (en première approximation des cercles). Tout point de la surface du mât peut être défini par le paramètre "hauteur" et le paramètre "angle" qui définit l'azimuth du point par rapport à l'axe du bateau.
Dans la surface de carène d'un bateau, les choses sont analogues, quoi que plus compliquées : en effet des coques composées de portions de surfaces planes, cylindriques, ou côniques, ont en général de piètres performances. Encore que, certains bateaux à coque à bouchain doivent pouvoir être décrits ainsi, et pourtant ils naviguent... Mais puisque nous nous intéressons aux coques dites "en forme", il faut d'autres outils pour les concevoir. Des surfaces comme les "B-Splines" ou encore les "NURBS" sont très utiles pour cela. On parlera par la suite de "NURBS" d'une manière générale : en effet les B-Splines ne sont qu'une variété particulière de NURBS, un peu comme les droites qui, pour les matheux, ne sont qu'une variété particulière de cercles à courbure nulle...
Les surfaces NURBS sont des surfaces paramétriques. Elles sont engendrées par des courbes paramétriques. Prenons un exemple de courbe paramétrique. Un enfant lance une balle à un autre. La trajectoire de la balle est, en première approximation (en supposant qu'ils jouent à balle dans le vide) une parabole. Les lois qui gouvernent le mouvement de la balle le long de sa trajectoire sont simples à exprimer : tout bachelier, même littéraire, se doit de les connaître. Si l'on représente cette trajectoire dans le plan vertical dans lequel elle s'inscrit, que l'on repère avec l'abscisse (x) et l'ordonnée (z), supposant le point d'origine de la trajectoire en (0, 0), et la vitesse à l'origine de la balle (Vx0, Vz0), elles s'expriment par les formules mathématiques suivantes, relatives au paramètre temps (t) :
Il est trivial (ou particulièrement douloureux pour certains lecteurs, à qui je demande de me pardonner), à partir des deux formules ci-dessus, d'exprimer le temps en fonction de l'abscisse x (t = x / Vx0), et en remplaçant dans la seconde formule d'obtenir une représentation purement spatiale (non paramétrée) de la trajectoire, à savoir, les quantités entre parenthèses étant des constantes :

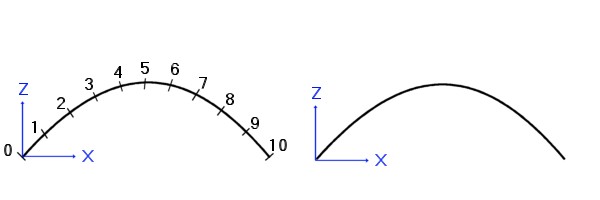
L'image ci-dessus illustre la différence entre ces deux modes de représentation. A gauche, la représentation paramétrique. On a porté sur la courbe dix points représentants dix valeurs régulièrement espacées du paramètre t (dans cet exemple, le temps écoulé depuis le lancement de balle en dixièmes de seconde). Cette représentation graphique correspond au modèle des deux premières formules (X et Z en fonction de t). Sur la courbe de droite, aucune référence au temps n'apparait. Elle correspond au modèle de la dernière formule (Z en fonction de X). On voit que la représentation paramétrique (avec t) est plus riche que la représentation purement géométrique (sans t). On pourrait, en reprenant cet exemple du lancer de balle, concevoir la différence de "contenu" entre les deux représentations en imaginant qu'il s'agit d'un lancer effectué par un joueur de basket. Dans un cas, s'il fait une passe à un coéquipier qui se trouve lancé dans sa course, il doit tenir compte du temps, s'il veut que sa passe arrive à destination au bon endroit et au bon moment. Dans un autre cas, s'il effectue un lancer vers le panneau en visant le panier, il se moque du temps et tout ce qui lui importe est la précision géométrique de la trajectoire pour qu'elle se termine là où il le souhaite.
Dans l'exemple ci-dessus, on conçoit bien que la donnée du vecteur de vitesse initiale de la balle suffit à définir complètement la courbe, puisque la balle pendant son vol est soumise aux lois de la physique, lesquelles ne sont pas quelconques. La parabole de la trajectoire est définie par deux polynomes en "t" de degré inférieur ou égal à deux : ont dit que la courbe paramétrique correspondante est "de degré deux". Dans cet exemple, le vecteur de vitesse de la balle à son arrivée est simple à déterminer : il s'agit de l'image dans un miroir du vecteur vitesse au départ.
Dans tout ce qui suit, lorsque nous parlerons de "B-Splines" (les plus simples des NURBS), nous allons considérer des courbes de degré trois. Dans le plan X-Z, une telle courbe s'exprime par la combinaison de deux expressions d'un même paramètre "U". Nous employons une lettre différente de "t" car il ne s'agit plus, ici, du paramètre "temps" de la physique.
X = ax . u3 + bx . u2 + cx . u + dx
Z = az . u3 + bz . u2 + cz . u + dz
Les deux expressions ci-dessus sont des polynomes. Par opposition, une courbe de type "rationnelle" serait décrites par deux expressions, X et Z, chacune étant une fraction avec un polynome au numérateur et un polynome au dénominateur. Avec les équations ci-dessus, il suffit, pour déterminer de manière non univoque la courbe correspondante dans l'espace, de fixer les huit valeurs des coefficients ax ... dz. Cela peut se faire de manière algébrique, comme ci-dessus, ce qui n'est pas très pratique. Il se trouve que cela peut aussi se faire de manière géométrique, en fixant :
Par commodité, en fixant l'origine du vecteur tangent au départ à (X0, Z0), on détermine son extrémité, à savoir le point (X1, Z1). De même, en fixant l'extrêmité du vecteur tangent à l'arrivée en (X3, Z3), cela définit son origine (X2, Z2). L'ensemble des quatre points (X0, Z0), (X1, Z1), (X2, Z2), (X3, Z3) définit un jeu de points de contrôle de la courbe. Voir l'image ci-dessous. Vous pouvez, avec votre souris, prendre les points de contrôle (petits carrés) sur cette courbe et les déplacer. Observez ce qui se passe.
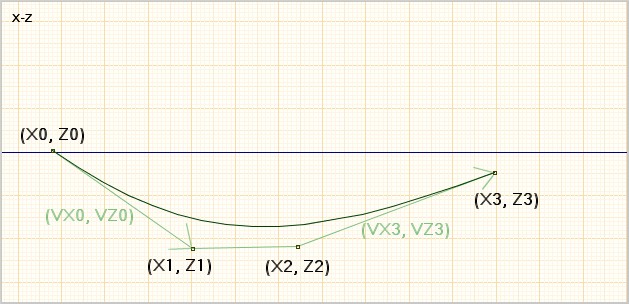
Comment ? Cela ne marche pas ? Pardonnez moi, c'est de ma faute : cette image n'est qu'une image statique. Recommencez avec l'applet ci-dessous ;)
Ca marche ? Ouf... je vais échapper à votre vindicte ! Comme vous pouvez le constater, on peut faire beaucoup de formes différentes en déplaçant les extrêmités et surtout les points de contrôle. Essayez donc de faire un quart de cercle parfait. Certes vous allez faire des choses qui ressemblent, mais le quart de cercle parfait n'est pas possible avec cette technique. Les matheux ne seront pas surpris : un cercle est une courbe paramétrique rationnelle, il n'est donc pas réalisable avec une B-spline (polynome) : il faudrait pour cela passer à la technique des NURBS, que nous verrons plus loin.
Pour raffraichir la mémoire des lecteurs matheux, les équations paramétriques d'un cercle
de rayon r décrit par un vecteur tournant d'angle au centre alpha
s'expriment par des fractions rationnelles, avec le paramètre t = sin (alpha/2) :
X = r . (1-t2) / (1+t2)
Z = r . 2t / (1+t2)
Une des difficultés des NURBS (ou des B-splines) en architecture navale tient au raccordement de courbes et de surfaces. Nous allons en voir un exemple sur deux courbes : la quille et l'étrave d'un bateau. Considérons l'applet suivant (pas de blague, c'en est vraiment un). La ligne bleue représente le niveau de l'eau. La courbe située vers le bas (réseau de contrôle vert) représente la vue en coupe de la partie inférieure de la coque d'un bateau. La courbe située à droite (réseau de contrôle rouge) représente la vue en coupe de l'étrave de la même coque de bateau. La ligne de bas de coque se raccorde à la ligne d'étrave dans une zone nommée "brion". Dans des schémas d'architecture modernes, il n'y a pas de point anguleux entre la ligne de bas de coque et l'étrave : le brion est arrondi. Et les surfaces de carène, au voisinage de ce brion, ne présentent pas de point anguleux ni de raccordement "plan sur plan" comme on en voit sur certains bateaux anciens ou à bouchains. Pour arriver à cela, il faut et il suffit que les deux courbes (bas de coque et étrave) soient tangentes à leur point de raccordement. En d'autre termes, le vecteur tangent à la fin de la ligne de bas de coque doit être aligné avec le vecteur tangent au début de l'étrave. Si ces deux vecteurs sont de longueurs différentes, il y a une rupture de "rayon de courbure" au voisinage du brion, ce qui est fréquent et, suivant l'amplitude de cette rupture, donne un "style" à la coque. Essayez : manipulez ces deux lignes et retrouvez des lignes du dix neuvième siècle, des lignes du vingt et unième : c'est possible.
Des surfaces paramétriques sont engendrées par deux familles de courbes, chaque famille étant paramétrée par un paramètre propre. En effet, du fait qu'une surface a une dimention de "deux", il faut deux paramètres. On appelera, dans la suite de ce site, "U" et "V" les paramètres de chacune de ces deux familles. Dans l'exemple de la surface de la mer, "U" pourrait être la latitude et "V" la longitude, la première famille de courbes est constituée des parallèles et la seconde des méridiens. Dans l'exemple du mât de bateau, "U" pourrait être la hauteur en dessus de la base et "V" l'azimuth : la première famille de courbes est constituée des génératrices, et la seconde des sections.
Comme dans l'exemple de la trajectoire de la balle vu plus haut, il faut bien voir la distinction entre le modèle mathématique (les deux familles de courbes paramétriques) et la surface qu'il permet d'engendrer. Cette dualité de représentation sera mieux comprise en regardant les deux images ci-dessous. Comme dans l'exemple de la trajectoire parabolique, on a à gauche une représentation paramétrique, et à droite une représentation purement spatiale du même objet : une coque. On conçoit bien qu'il ne s'agit pas de la même approche de définition, bien qu'il s'agisse du même objet.
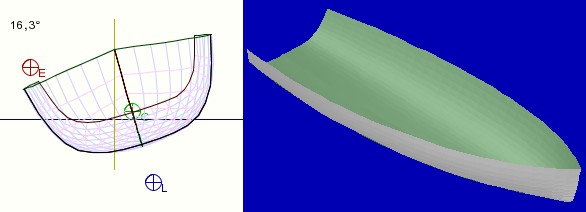
Remarque : un examen attentif de la vue spatiale montre des "facettes" assez clairement visibles avec le dégradé de couleur. C'est en effet qu'on est passé d'une représentation paramétrique, mathématiquement exacte telle que celle qui est stylisée à gauche, à un modèle spatial approximatif en facettes triangulaires planes, lequel est rendu en perspective à droite.
La démarche de ce site est donc la suivante : on veut obtenir ce qu'on voit à droite (une surface de carène) et pour cela on passe par ce qu'on voit à gauche (deux réseaux de courbes paramétriques qui définissent une surface paramétrique). Problème vieux comme le monde, qui s'est posé aux architectes, aux charpentiers, aux ingénieurs : passer de la réalité à un modèle, travailler sur le modèle, revenir à la réalité. Que nul n'entre ici s'il n'est géomètre, disait Platon...
Pour en terminer et préciser un peu le vocabulaire, les surfaces NURBS sont engendrées par des courbes particulières, dites "Non Uniform Rational B-Splines", dont l'expression algébrique est une fraction de deux polynomes. Les surfaces B-Spline sont un cas particulier des surfaces NURBS dans lequel le dénominateur de la fonction est une constante, ce qui revient à dire que chaque fonction des paramètres "U" et "V" est un polynome de degré n. L'appellation B-Spline est un terme anglo-saxon, les francophones parlant aussi de "courbes de Bézier", du nom de l'ingénieur de la société Renault qui a utilisé le premier ces courbes pour concevoir des carrosseries de voitures. On verra plus loin que les NURBS présentent l'avantage, par rapport aux B-Splines, de pouvoir réaliser des formes de surface présentant des irrégularités de courbure importantes.
La différence entre les NURBS et les B-splines, importante, sera explicitée dans une version ultérieure de ce site qui, pour l'instant, ne gère que des B-splines. Un peu de patience...
En résumé :
Une surface paramétrique est engendrée par deux familles de courbes dans l'espace. Chaque courbe de ces famille est elle même une courbe paramétrique, à savoir que les coordonnées de tout point de cette courbe sont définies par des expressions algébriques en fonction d'un paramètre. On dénomme par la suite ces paramètres "U" et "V". Lorsque ces expressions algébriques sont de simples polynomes de degré n, on parle de courbes B-Splines. Lorsque ces expressions algébriques sont des fractions rationnelles (rapport de deux polynomes), on parle de courbes NURBS, pour "Non Uniform Rational B Splines". La définition d'une courbe NURBS ne nécessite qu'un faible nombre de paramètres, et il en est donc de même de la définition d'une surface NURBS. Le nombre réduit de ces paramètres permet de gagner du temps dans l'élaboration du modèle d'une carène, notamment parce qu'il existe des méthodes graphiques de réglage de ces paramètres, à partir d'un jeu réduit de "points de contrôle".